Android Studio NDK 如何生成so
本文共 1120 字,大约阅读时间需要 3 分钟。
Android Studio NDK 如何生成so
先来看下代码
MyNdkUtil.javapackage com.heiko.ndksotest;public class MyTestNdk { static { System.loadLibrary("native-lib"); } public native String stringFromJNI();} native-lib.cpp
#include#include extern "C"JNIEXPORT jstring JNICALLJava_com_heiko_ndksotest_MyTestNdk_stringFromJNI(JNIEnv *env, jobject instance) { /*std::string hello = "Hello from C++ !"; return env->NewStringUTF(hello.c_str());*/ char* hello = "Hello from C++ !!"; return env->NewStringUTF(hello);}
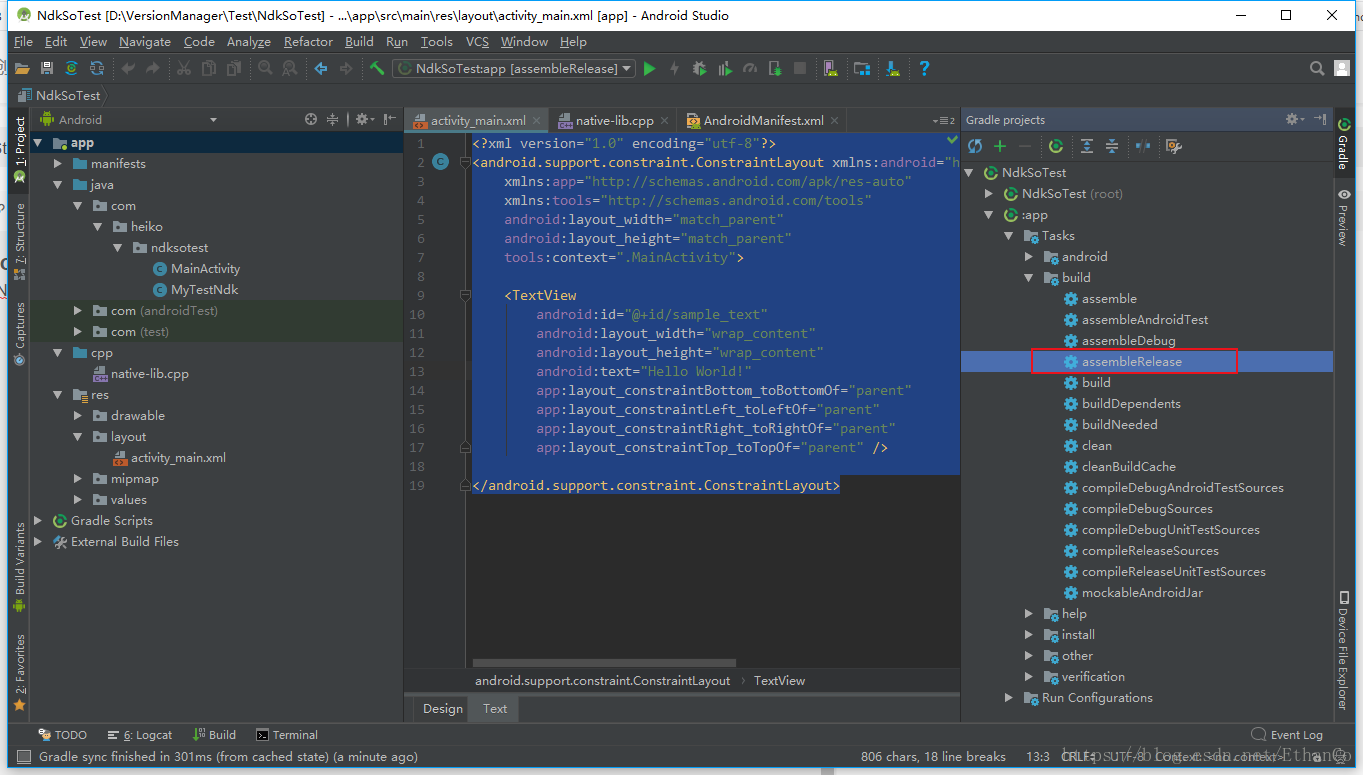
接着,编译NDK项目
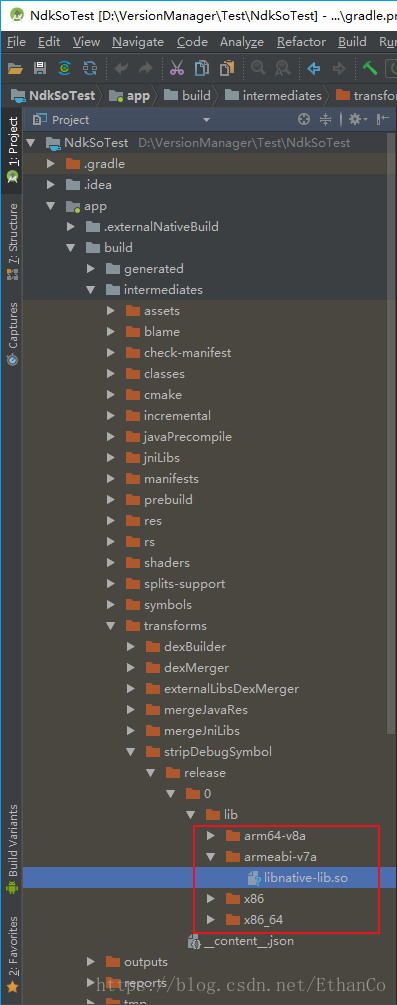
然后,在项目中找到so文件
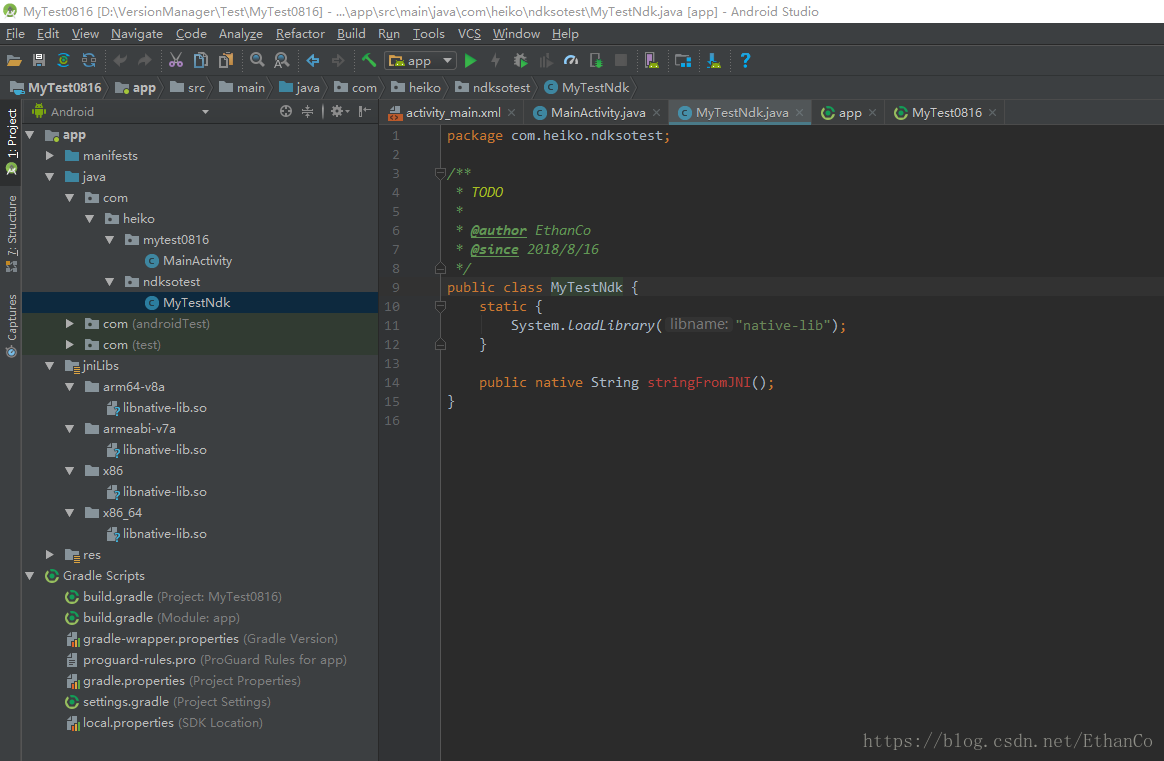
接着,将so及MyTestNdk.java复制到另外的项目中使用
其中,MyTestNdk.java的包名必须与原报名一致。
值得一提的是,在正式的环境中,一般会将这些java文件打包成jar包,将jar及so文件直接提供给调用者使用。最后,在MainActivity.java中调用并运行
public class MainActivity extends AppCompatActivity { @Override protected void onCreate(Bundle savedInstanceState) { super.onCreate(savedInstanceState); setContentView(R.layout.activity_main); TextView tv = (TextView) findViewById(R.id.sample_text); MyTestNdk myTestNdk = new MyTestNdk(); tv.setText(myTestNdk.stringFromJNI()); }} App界面显示 Hello from C++ !!,至此调用成功。
你可能感兴趣的文章
NAS个人云存储服务器搭建
查看>>
NAS服务器有哪些优势
查看>>
NAT PAT故障排除实战指南:从原理到技巧的深度探索
查看>>
nat 网卡间数据包转发_你是不是从来没有了解过光纤网卡,它跟普通网卡有什么区别?...
查看>>
NAT-DDNS内网穿透技术,快解析DDNS的优势
查看>>
NAT-DDNS内网穿透技术,快解析DDNS的优势
查看>>
NAT-DDNS内网穿透技术,解决动态域名解析难题
查看>>
natapp搭建外网服务器
查看>>
NativePHP:使用PHP构建跨平台桌面应用的新框架
查看>>
nativescript(angular2)——ListView组件
查看>>
NativeWindow_01
查看>>
Native方式运行Fabric(非Docker方式)
查看>>
Nature | 电子学“超构器件”, 从零基础到精通,收藏这篇就够了!
查看>>
Nature和Science同时报道,新疆出土四千年前遗骸完成DNA测序,证实并非移民而是土著...
查看>>
Nature封面:只低一毫米,时间也会变慢!叶军团队首次在毫米尺度验证广义相对论...
查看>>
Nat、端口映射、内网穿透有什么区别?
查看>>
Nat、端口映射、内网穿透有什么区别?
查看>>
nat打洞原理和实现
查看>>
NAT技术
查看>>
NAT模式/路由模式/全路由模式 (转)
查看>>